Shikra
| Shikra | |
|---|---|

| |
| Adult female (dussumieri) | |
| Scientific classification | |
| Domain: | Eukaryota |
| Kingdom: | Animalia |
| Phylum: | Chordata |
| Class: | Aves |
| Order: | Accipitriformes |
| Family: | Accipitridae |
| Genus: | Accipiter |
| Species: | A. badius
|
| Binomial name | |
| Accipiter badius (Gmelin, JF, 1788)
| |
| Subspecies | |
| |
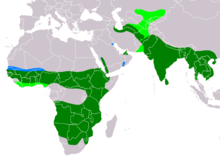
| Range of A. badius Breeding Resident Non-breeding
| |
| Synonyms | |
|
Astur badius | |
The shikra (Accipiter badius) is a small bird of prey in the family Accipitridae found widely distributed in Asia and Africa where it is also called the little banded goshawk. The African forms may represent a separate species but have usually been considered as subspecies of the shikra. The shikra is very similar in appearance, as well as behavior, at least to some degree, to other Accipiter species including the Chinese goshawk (Accipiter soloensis), Eurasian goshawk (Accipiter gentilis) and Eurasian sparrowhawk (Accipiter nisus). They have a sharp two note call and have the typical flap and glide flight. Their calls are imitated by drongos and the common hawk-cuckoo resembles it in plumage.
Taxonomy
[edit]The shikra was formally described in 1788/1789 by the German naturalist Johann Friedrich Gmelin in his revised and expanded edition of Carl Linnaeus's Systema Naturae. He placed it with the eagles, hawks and relatives in the genus Falco and coined the binomial name Falco badius.[2] Gmelin description was based on the "brown hawk" from Ceylon that had been described and illustrated in 1776 by the English naturalist Peter Brown.[3] The shikra is now one of 49 species placed in the genus Accipiter that was introduced in 1760 by the French zoologist Mathurin Jacques Brisson.[4][5] The genus name is Latin for "hawk", from accipere, "to grasp". The specific epithet badius is Latin for "chestnut-coloured" or "brown".[6]
Six subspecies are recognised:[5]
- A. b. sphenurus (Rüppell, 1836) – Senegal and Gambia to southwest Arabia south to north Tanzania and north DR Congo
- A. b. polyzonoides Smith, A, 1838 – south DR Congo and south Tanzania to South Africa
- A. b. cenchroides (Severtsov, 1873) – Caucasus to central Asia and northwest India
- A. b. dussumieri (Temminck, 1824) – central India and Bangladesh
- A. b. poliopsis (Hume, 1874) – north India to south China, Indochina and north Sumatra
- A. b. badius (Gmelin, JF, 1788) – southwest India and Sri Lanka
Description
[edit]
The shikra is a small raptor (26–30 cm long) and like most other Accipiter hawks, this species has short rounded wings and a narrow and somewhat long tail. Adults are whitish on the underside with fine rufous bars while the upperparts are grey. The lower belly is less barred and the thighs are whitish. Males have a red iris while the females have a less red (yellowish orange) iris and brownish upperparts apart from heavier barring on the underparts. The females are slightly larger. The mesial stripe on the throat is dark but narrow. In flight the male seen from below shows a light wing lining (underwing coverts) and has blackish wing tips. When seen from above the tail bands are faintly marked on the lateral tail feathers and not as strongly marked as in the Eurasian sparrowhawk. The central tail feathers are unbanded and only have a dark terminal band.[7] Juveniles have dark streaks and spots on the upper breast and the wing is narrowly barred while the tail has dark but narrow bands. A post juvenile transitional plumage is found with very strong barring on the contour feathers of the underside.[8] The call is pee-wee, the first note being higher and the second being longer. In flight the calls are shorter and sharper kik-ki ... kik-ki. The Chinese sparrowhawk is somewhat similar in appearance but has swollen bright orange ceres and yellow legs with the wing tips entirely black.[9][10]
Subspecies cenchroides is larger and paler and found in Turkestan, Afghanistan and eastern Iran. The Indian population dussumieri is resident on the plains and lower hills (up to 1400 m in the Himalayas). The nominate form is found in Sri Lanka and has somewhat darker grey upperparts. The Burmese shikra A. b. poliopsis may represent a distinct species. The population on the island of Car Nicobar, earlier treated as a subspecies butleri[11] and that on Katchal Island, obsoletus are now treated as a sub-species within a full species, the Nicobar sparrowhawk (Accipiter butleri).[9][12] The west African population A. b. sphenurus is migratory while the southern African A. b. polyzonoides is more nomadic in its movements. In Asia only A. b. cenchroides is migratory.[8]
Behaviour and ecology
[edit]The shikra is found in a range of habitats including forests, farmland and urban areas. They are usually seen singly or in pairs. The flight is typical with flaps and glides. During the breeding season pairs will soar on thermals and stoop at each other. Their flight usually draws alarms among smaller birds and squirrels. They feed on rodents (including Meriones hurrianae[13]), squirrels, small birds, small reptiles (mainly lizards but sometimes small snakes[14]) and insects.[12] Small birds usually dive through foliage to avoid a shikra and a Small Blue Kingfisher has been observed diving into water to escape. Babblers have been observed to rally together to drive away a shikra.[15] They will descend to the ground to feast on emerging winged termites,[16] hunt at dusk for small bats[17] (such as Cynopterus sphinx[18][19]) and in rare instances they may even resort to feed on carrion.[20] In one instance a male was found feeding on a dead chick at the nest.[21] Their calls are mimicked by drongos and this behaviour is thought to aid in stealing food by alarming other birds that the drongos associate with.[22][23]
Breeding
[edit]
The breeding season in India is in summer from March to June. The nest is a platform similar to that of crows lined with grass. Both sexes help build the nest, twigs being carried in their feet.[24] Like crows, they may also make use of metal wires.[25] The usual clutch is 3 to 4 eggs (when eggs are removed they lay replacements and one observer noted that they could lay as many as 7 in a season[26]) which are pale bluish grey stippled on the broad end in black. The incubation period is 18 to 21 days.[12]
In culture
[edit]The shikra was a favourite among falconers in India and Pakistan due to the ease with which it could be trained and was frequently used to procure food for the more prized falcons. They were noted for their pluck and ability to take much larger birds including partridges, crows and even young peafowl.[12][27][28] The word shikra or shikara means hunter in the Hindi language (the male was called chipak or chipka based on call[29]) The word Shikra is borrowed from the Urdu word (شِـكْـره) which is derived from the word shikari (شِكارى) meaning hunter.[30]
The word is also used in the French name Le Chicquera which was however given to the red-necked falcon by Levaillant in 1799.[31][32][33]
Famous Punjabi poet Shiv Kumar Batalvi wrote a poem called "Main Ik Shikra Yaar Banaya" about a lost love wherein he compares her to a shikra.[34][35]
Gallery
[edit]-
Shikra bird, Pune
-
Male at Pune (Maharashtra), India
-
Male at Chandigarh, India
-
Juvenile at Chandigarh, India
-
Female with a kill
-
In flight
-
At Bangalore, India
-
Bangalore, India
-
Shikra in Gurgaon,India
-
Shikra in Gurgaon,India
-
Immature feeding on Calotes versicolor
-
In Chandigarh
References
[edit]- ^ BirdLife International (2019). "Accipiter badius". IUCN Red List of Threatened Species. 2019: e.T22695490A155445348. doi:10.2305/IUCN.UK.2016-3.RLTS.T22695490A155445348.en. Retrieved 12 November 2021.
- ^ Gmelin, Johann Friedrich (1788). Systema naturae per regna tria naturae : secundum classes, ordines, genera, species, cum characteribus, differentiis, synonymis, locis (in Latin). Vol. 1, Part 1 (13th ed.). Lipsiae [Leipzig]: Georg. Emanuel. Beer. p. 280.
- ^ Brown, Peter (1776). Nouvelles illustrations de zoologie : contenant cinquante planches enlumineés d'oiseaux curieux, et qui non etés jamais descrits, et quelques de quadrupedes, de reptiles et d'insectes, avec de courtes descriptions systematiques [New illustrations of zoology, containing fifty coloured plates of new, curious, and non-descript birds, with a few quadrupeds, reptiles and insects]. London: Imprimé pour B. White. p. 6; Plate 3.
- ^ Brisson, Mathurin Jacques (1760). Ornithologie; ou, Méthode contenant la division des oiseaux en ordres, sections, genres, espéces & leurs variétés (in French). Vol. 1. Paris: Jean-Baptiste Bauche. pp. 28, 310.
- ^ a b Gill, Frank; Donsker, David; Rasmussen, Pamela, eds. (August 2022). "Hoatzin, New World vultures, Secretarybird, raptors". IOC World Bird List Version 12.2. International Ornithologists' Union. Retrieved 5 December 2022.
- ^ Jobling, James A. (2010). The Helm Dictionary of Scientific Bird Names. London: Christopher Helm. p. 30, 65. ISBN 978-1-4081-2501-4.
- ^ Mees, GF (1981). "The Sparrow-Hawks (Accipiter) of the Andaman Islands". J. Bombay Nat. Hist. Soc. 77 (3): 371–412.
- ^ a b Herremans M & Louette, M (2000). "A partial post-juvenile molt and transitional plumage in the shikra (Accipiter badius) and Grey Frog Hawk (Accipiter soloensis)" (PDF). Journal of Raptor Research. 34 (4): 249–261.
- ^ a b Rasmussen PC & Anderton, JC (2005). Birds of South Asia. The Ripley Guide. Volume 2. Smithsonian Institution and Lynx Edicions. p. 97. ISBN 8487334660.
- ^ Blanford WT (1895). The Fauna of British India, Including Ceylon and Burma. Birds. Volume 3. London: Taylor and Francis. pp. 398–400.
- ^ Gurney JH (1859). "Bulletin of the British Ornithologists Club. No 50 (January 30th, 1898)". Ibis. 4 (seventh series): 290–291. doi:10.1111/j.1474-919X.1898.tb05529.x.
- ^ a b c d Ali S; Ripley & S D (1978). Handbook of the Birds of India and Pakistan. Volume 1 (2nd ed.). New Delhi: Oxford University Press. pp. 234–239. ISBN 0-19-565506-0.
- ^ Kankane, PL (1996). "Strange death of a shikra". J. Bombay Nat. Hist. Soc. 96: 140–141.
- ^ Jha, Samiran (2002). "Attempted feeding by a shikra Accipiter badius family Accipitridae, on buffstriped keelback Amphiesma stolata, family Colubridae". J. Bombay Nat. Hist. Soc. 99 (2): 298.
- ^ Osmaston, BB (1923). "The Shikra Astur badius". J. Bombay Nat. Hist. Soc. 29 (2): 560–561.
- ^ Himmatsinhji MK (1986). "Peculiar feeding behaviour of the Shikra Accipiter badius (Gmelin) and the Honey Buzzard Pernis ptilorhyncus (Temminck)". J. Bombay Nat. Hist. Soc. 83 (4): 201–202.
- ^ Mikula, P.; Morelli, F.; Lučan, R. K.; Jones, D. N.; Tryjanowski, P. (2016). "Bats as prey of diurnal birds: a global perspective". Mammal Review. 46 (3): 160–174. doi:10.1111/mam.12060.
- ^ Muni, Manoj; Hegde, Vithoba (1998). "Indian Shikra preying on Short-nosed Fruit Bats". J. Bombay Nat. Hist. Soc. 95 (2): 338–339.
- ^ Zarri, AA (2001). "More information on shikra Accipiter badius (Gmelin) feeding on shortnosed fruit bats Cynopterus sphinx Vahl". J. Bombay Nat. Hist. Soc. 98 (1): 106–107.
- ^ Naoroji, Rishad (1991). "Shikra Accipiter badius taking carrion". J. Bombay Nat. Hist. Soc. 88 (3): 447–448.
- ^ Kittur, S & Gopi Sundar, K S (2010). "Cronism by the Shikra Accipiter badius". Forktail. 26: 140–141.
- ^ Serrao JS (1975). "Behaviour-pattern mimicry by a Goldfronted Chloropsis, and some thoughts on it". Newsletter for Birdwatchers. 15 (3): 4–5.
- ^ Flower, Tom (2010). "Fork-tailed drongos use deceptive mimicked alarm calls to steal food". Proc. R. Soc. B. 278 (1711): 1548–1555. doi:10.1098/rspb.2010.1932. PMC 3081750. PMID 21047861.
- ^ Phillips, WWA (1933). "Some observations on the nesting of a pair of Ceylon Shikra Hawks (Astur badius badius Gmelin)". J. Bombay Nat. Hist. Soc. 36 (2): 509–511.
- ^ Lowther, EHN (1944). "Volume 45". Journal of the Bombay Natural History Society. 45 (1): 5–16.
- ^ Biddulph, CH (1937). "Number of eggs laid by the Indian Shikra [Astur badius dussumieri (Temm. & Lang.)]". J. Bombay Nat. Hist. Soc. 39 (2): 406.
- ^ Whistler, Hugh (1949). Popular Handbook of Indian Birds (4th ed.). Gurney & Jackson. pp. 380–382.
- ^ Jerdon, TC (1862). The birds of India. Volume 1. Calcutta: Military Orphan Press. pp. 48–50.
- ^ Blyth, Edward (1849). Catalogue of the Birds in the Museum Asiatic Society. Asiatic Society, Calcutta. p. 23.
- ^ Al-Haj Ibrahim, Hassan, Birds of prey (Manuscript in Arabic
- ^ Radcliffe, E Delme (1871). Notes on the falconidae used in India in falconry. Mills and Son, Southsea. pp. 29–30.
- ^ Balfour, EG (1885). The Cyclopaedia of India. Vol. 2 (3rd ed.). London: Bernard Quaritch. p. 26.
- ^ Jobling, James (2010). The Helm Dictionary of scientific bird names (PDF). London: Christopher Helm. p. 100. ISBN 978-1408125014.
- ^ "माए नी माए मैं इक शिकरा यार बणाया - शिव कुमार बटालवी".
- ^ "How to Gender a Hawk ("Shikkra"): A look at a Shiv Kumar Batalvi poem".
External links
[edit]- (Shikra = ) Little banded goshawk – Species text in The Atlas of Southern African Birds
- photographs and videos













